www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Bahas Soal Matematika » Logaritma ›
Sebuah lingkaran memiliki jari-jari \( \log a^2 \) dan keliling \( \log b^4 \), maka \( {}^a \! \log b = \cdots \)
- \( \frac{1}{4\pi} \)
- \( \frac{1}{\pi} \)
- \( \pi \)
- \( 2\pi \)
- \( 10^{2\pi} \)
Pembahasan:
Rumus keliling lingkaran adalah \( 2 \pi r \), sehingga berlaku:
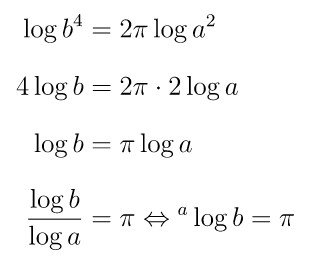
Jawaban C.